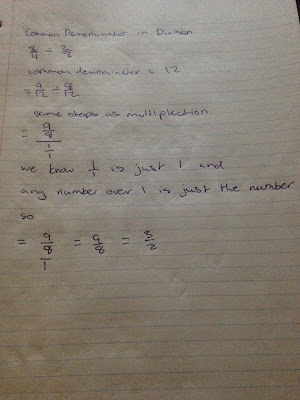When it comes to 3D shapes, they are everywhere, but understanding them in the classroom can be difficult. That's why we used a guiding learning activity in order to complete our task. The activity simply helped us solve the bigger picture by taking us through the problem step by step and explaining the to find the little things and put it together to find a bigger answer. The learning activity used physical manipulatives like string to measure the circumference of a circle and a toilet paper roll to represent a cylinder. We first used the cylinder and dipped the ends in ink and created our circle on the paper. We used the string to find the circumference of the circle as well find the area. Then we cut the cylinder in half from end to end, creating a rectangle. Then we used the rectangles sides to finds it area. Boom you have the surface area. The problem continues getting more and more complex as the steps continue. As a pre-service teacher this activity can be a great tool when working with students. An activity like this can be used in a variety of classrooms, not just for math and the step by step thinking is a great strategy for students to grasp. Sometimes rushing to the answer is not the best idea, I would know.
The technique of physical manipulatives has been used in my placement class often. Just this week my associate teacher was using the string technique to show that circumference was simply a length and its relevance to pi. When a circles diameter is 1, its circumference is pi. This can be easily represented with the string, especially for those learners who are curious to know what the significance of 3.14... or pi is. The students had a better understand of the concepts of pi and circumference and its significance.
Another Cool Way to measure Circumference
The video above shows another cool way to measure circumference when you don't have string available. I found this way a lot easier in my opinion.
Finally I wanted to talked about distinguishing 2D and 3D shapes and why its important to use a physical manipulative or technological tool to represent the shapes. When a shape is just on a paper its often hard to distinguish, especially at the younger grades. I mean how do you represent the difference between a sphere and a circle on paper. They look almost the same. Having the physical manipulatives like having a sphere such as tennis ball or baseball versus a circle like a plate can really show the difference in shapes. This goes for all the shapes including a triangle and pyramid, it makes it easy for your learners to grasp the concepts of dimensions.
Monday, November 21, 2016
Monday, November 14, 2016
Dimensions, not the scary type!
The past week in math class we talked about geometry and spatial sense, discussing everything about two and three dimensional shapes. I considered myself pretty good when it comes to geometry, angles and special sense as I am able to relate sports and math, particularly geometry and angles. I am a sports and physical education major after all. Forgive the "Like Mike" reference but that is how I understood the difference the three types of triangles. For example, the greatest team in basketball history the 1995-1996 Chicago Bull used a "triangle" offence in certain situations. The goal of this offence was to isolate for the great Michael Jordan, moving all players to the outside so he can take it to the basket with limited defenders in the area. Now when you think about the word I just used, "isolate", does it remind you of a triangle? Yes! Isosceles triangle, the triangle with 2 equal angles and two equal sides, and Michael Jordan at the tip running the play. Once its drawn out on the basketball court it is really easy to see.
Like Mike Geometry
Now knowing the basketball offences could be a little difficult for some to understand, but the court itself also has some interesting shapes. Other sports also use some interesting shapes, take a traditional soccer ball for example. Its made of both pentagons and hexagons. Even something like a swimming pool is shaped in a prism. It is quite easy to relate different geometric shapes and different sports. Maybe students I have in my placement learn the same way as me and I will be able to relate to them in the geometry units.
Finally I liked the use of manipulatives in our geometry class. The exercise where we had to create different shapes using smaller or more shapes was great for understanding spatial sense and provides a manipulative for those learners who work better with contact. This activity also addresses the analysis of shapes, helping learners discover similarities and differences in shapes and create different groupings of these shapes.
Like Mike Geometry
Now knowing the basketball offences could be a little difficult for some to understand, but the court itself also has some interesting shapes. Other sports also use some interesting shapes, take a traditional soccer ball for example. Its made of both pentagons and hexagons. Even something like a swimming pool is shaped in a prism. It is quite easy to relate different geometric shapes and different sports. Maybe students I have in my placement learn the same way as me and I will be able to relate to them in the geometry units.
Finally I liked the use of manipulatives in our geometry class. The exercise where we had to create different shapes using smaller or more shapes was great for understanding spatial sense and provides a manipulative for those learners who work better with contact. This activity also addresses the analysis of shapes, helping learners discover similarities and differences in shapes and create different groupings of these shapes.
Monday, November 7, 2016
Working in Groups!!
Today, I am going to step away from talking about what was learned in class this week and transition my blog towards what I experienced in math during my placement this past structured experience day. My students are extremely hard working and in Grade 8, and they are focused on good grades and understanding math for when the move to secondary school. Many students want to be on the "honour role" and achieve academic excellence. They are motivated. The students have an upcoming mid-chapter test on patterning and algebra, something many of the students are not too strong with. However, there are students who excel at this strand of math and are great leaders in the classroom. This is when I was able to take what I learned in math class at Brock and apply it to my classroom. My associate teacher (I helped!!!) used something called conferencing ( or similar) which was simply putting the students into groups and having them work together, creating discussion and a great learning environment.
When the students were grouped they were assigned specific questions to work on as a team, and were grouped fairly and evenly so that some weaker students had the help of the stronger students. The groups transferred there work to chart paper and posted it for the class to see. What I really liked about this method is that a lot of the time, the students were engaged, often splitting the workload, completing the question and then discussing the reasoning behind this answer. This is a great tool for a peer evaluation as they are able to see the different strategies students in the group, as well as in other groups, used to find a solution. Also, the students were able to correct each other if there were mistakes, allowing them to see what they did wrong and gain another perspective. If I had one complaint it would be that sometimes, those who understand it more, would take over, and want to finish quickly. this takes away from the other learners as they are not able to try the problems themselves, they are simply observing the other students do the work.
Overall the group work ran smoothly, they were able to complete the review questions and post their solutions on the wall as reference. Being able to see specific strategies used by the students helped me understand their learning style as well as helped the other students with differentiated solutions.
Below are some of the work that they did.
When the students were grouped they were assigned specific questions to work on as a team, and were grouped fairly and evenly so that some weaker students had the help of the stronger students. The groups transferred there work to chart paper and posted it for the class to see. What I really liked about this method is that a lot of the time, the students were engaged, often splitting the workload, completing the question and then discussing the reasoning behind this answer. This is a great tool for a peer evaluation as they are able to see the different strategies students in the group, as well as in other groups, used to find a solution. Also, the students were able to correct each other if there were mistakes, allowing them to see what they did wrong and gain another perspective. If I had one complaint it would be that sometimes, those who understand it more, would take over, and want to finish quickly. this takes away from the other learners as they are not able to try the problems themselves, they are simply observing the other students do the work.
Overall the group work ran smoothly, they were able to complete the review questions and post their solutions on the wall as reference. Being able to see specific strategies used by the students helped me understand their learning style as well as helped the other students with differentiated solutions.
Below are some of the work that they did.
Monday, October 31, 2016
integers, not a negative experience
First, I am really happy we spent a great deal of time on fractions. I feel as if they are some of the hardest problems in elementary math and finding a way to show the simply way to an answer of a difficult question really makes my job as a teacher easy and it makes sure I can benefit my students. Like I have said before differentiated learning is something that needs to be understood by the teacher, there are many different students who learn a different way than you do and it is your job as the teacher to explore all ways to present and solve a problem. After all, you want your students to succeed, but also understand the problem.
I really enjoyed the mini conference activity. Not only did we get to share our ideas from the "Kitty Cat Problem" but we also had examples from other students in a previous session or class. Since our group solved the problem one way we were able to pair with another group in a "conference" and see the way they solved the problem. This helped us understand how other people see the problem, and when they explain their thought process we are able to see another a solution to the same answer. We went around to look at some other examples of the same question solved a completely different way. It was actually amazing how many different ways were expressed. One way which I will post below was actually so simple and so smart that I completely overlooked that way when completing the question myself. It goes to show when you are tough a certain way, you tend to avoid other ways of doing a question which I myself am really working on in order to show my students all possible solutions.
Below are the solutions that my group did and another groups solution done a completely different way. The point of the question was to find which store sold cat food a cheaper price.
Tuesday, October 25, 2016
Continuing Fractions
Last week we continued with fractions, continuing to make them less and less complicated for ourselves and later our students. I guess you can say this is the second 1/2 to the lesson (see what I did there).
One of the big topics this week was division of fractions, pretty scary as we approach Halloween. But of course, there is always a simpler way to do things than the way we have been taught. Most of us had been taught that you only find a common denominator for multiplication of fraction right? Well despite being told no you can't do it, you can actually find a common denominator to help divide fractions easier. When I first heard this of course I was thinking, no not possible I haven't been taught that way. Well consider the following problem. I will go through step by step how to solve it.
Maintaining an open mind when coming to class is really important when attempting to understand new concepts. For someone like myself, I find that extremely hard, I guess you could say I am fairly close-minded when it comes to certain things. I am working really hard to fix that because I want to show my students all the ways to solve different problems because teaching them one way will not be enough for some learners. Every student is different and many of them will not learn the same way as the other so its important to understand different ways to find the same answer. It will help you personally become a better teacher.
Continuing with the lesson we also reviewed six steps to creating an open question, a question that allows the learner to make decisions. These six steps are:
1. Begin with answer.
2. Ask for similarities.
3. Leave certain information out of the problem.
4. Provide several numbers and math words. The students will have to create the problem using the numbers and words.
5. Use soft language.
6. Prove that an idea is true or false.
A simple example would be using the number 43 and the word sum, create a work problem that has fraction as the answer. An answer could be Jimmy has 21 green apples and 22 red apples that add to a sum of 43 apples total, he has 21/43 green and 22/ 43 red which can be expressed as a ratio of 21:22.
Overall the lesson was really great, I learned another new concept which I look forward to applying in my classroom during my placement block.
One of the big topics this week was division of fractions, pretty scary as we approach Halloween. But of course, there is always a simpler way to do things than the way we have been taught. Most of us had been taught that you only find a common denominator for multiplication of fraction right? Well despite being told no you can't do it, you can actually find a common denominator to help divide fractions easier. When I first heard this of course I was thinking, no not possible I haven't been taught that way. Well consider the following problem. I will go through step by step how to solve it.
Maintaining an open mind when coming to class is really important when attempting to understand new concepts. For someone like myself, I find that extremely hard, I guess you could say I am fairly close-minded when it comes to certain things. I am working really hard to fix that because I want to show my students all the ways to solve different problems because teaching them one way will not be enough for some learners. Every student is different and many of them will not learn the same way as the other so its important to understand different ways to find the same answer. It will help you personally become a better teacher.
Continuing with the lesson we also reviewed six steps to creating an open question, a question that allows the learner to make decisions. These six steps are:
1. Begin with answer.
2. Ask for similarities.
3. Leave certain information out of the problem.
4. Provide several numbers and math words. The students will have to create the problem using the numbers and words.
5. Use soft language.
6. Prove that an idea is true or false.
A simple example would be using the number 43 and the word sum, create a work problem that has fraction as the answer. An answer could be Jimmy has 21 green apples and 22 red apples that add to a sum of 43 apples total, he has 21/43 green and 22/ 43 red which can be expressed as a ratio of 21:22.
Overall the lesson was really great, I learned another new concept which I look forward to applying in my classroom during my placement block.
Tuesday, October 18, 2016
Another interesting Lesson/ Fractions
The last class was another new experience for me, bringing new topic and teaching methods to my attention, as well as different ways to solve a single problems. the classes focus this week was fractions and all of the different parts and aspects of teaching and learning the topic if fractions in class. What I found important about the lesson on fractions is how easily relatable it is to real-life situations, which is what we want in order to keep the class involved and help them understand the importance of the lesson.
Take the example of 1/4 or 1 quarter. How many ways can you express that?
25%, 12 to 3 on the clock, which relates to people saying "a quarter after 6", 25 cents of the dollar etc.
A simple fraction related to 3 different things easily.
We then went into the addition and subtraction of fractions and how to explain why we don't add the denominators when adding (because it is a part of a whole) and the overall definition of a fraction to explain to our class.
Definition: a part of a whole number
Characteristics: numerator, denominator, division, percentage, ratio
Examples: 1/4, 25%, 0/4, 4/1
Non- Examples: 14
What I liked was the discussion of what us as teachers want our questions to lead to, our question goals. This had me thinking what I want personally out of the questions I ask during class time. Fearless speaking and sharing is something I consider important. I want my students to be able to discuss together as a group and as a class, even with me, aspects of the problem. When in a group and they are sharing their ideas the different types learners will be able to collaborate, which will lead to various answers and inclusion. This also evokes thinking, because having open questions there will be different answers and when the different earners are discussing their answers, they will be able to see the questions the different ways their peers do.
Finally, I really enjoy using physical manipulatives, because I was never given the opportunity to learn this way, I am able to take these ideas and apply them to my class room along with some of the learning styles I have from when I was in school.
The pictures above are simples ways to have students represent fractions using physical manipulatives that can be found almost anywhere. Chocolate also works great!
Overall the lesson on fractions was intriguing, learning different ways to express fractions and represent them in real-life is new to me, because of the way I have been taught, meaning I am both learning as a student (ways to do these myself) and as a teacher (ways to incorporate into the classroom).
Take the example of 1/4 or 1 quarter. How many ways can you express that?
25%, 12 to 3 on the clock, which relates to people saying "a quarter after 6", 25 cents of the dollar etc.
A simple fraction related to 3 different things easily.
We then went into the addition and subtraction of fractions and how to explain why we don't add the denominators when adding (because it is a part of a whole) and the overall definition of a fraction to explain to our class.
Definition: a part of a whole number
Characteristics: numerator, denominator, division, percentage, ratio
Examples: 1/4, 25%, 0/4, 4/1
Non- Examples: 14
What I liked was the discussion of what us as teachers want our questions to lead to, our question goals. This had me thinking what I want personally out of the questions I ask during class time. Fearless speaking and sharing is something I consider important. I want my students to be able to discuss together as a group and as a class, even with me, aspects of the problem. When in a group and they are sharing their ideas the different types learners will be able to collaborate, which will lead to various answers and inclusion. This also evokes thinking, because having open questions there will be different answers and when the different earners are discussing their answers, they will be able to see the questions the different ways their peers do.
Finally, I really enjoy using physical manipulatives, because I was never given the opportunity to learn this way, I am able to take these ideas and apply them to my class room along with some of the learning styles I have from when I was in school.
The pictures above are simples ways to have students represent fractions using physical manipulatives that can be found almost anywhere. Chocolate also works great!
Overall the lesson on fractions was intriguing, learning different ways to express fractions and represent them in real-life is new to me, because of the way I have been taught, meaning I am both learning as a student (ways to do these myself) and as a teacher (ways to incorporate into the classroom).
Sunday, October 2, 2016
Week Sept. 27.
Hey everyone!!!
So today was my learning activity presentation. I had the topic of whole number operations. Honestly I was really nervous going first and all so I'm hoping it went well. Using what I learned in the class previous, and in other classes I am taking; I decided to gamify the topic and activity in order to grasp the attention of my fellow classmates. I related it to a real life situation (even though it was fictional) and based the question I had on that real life situation. I created a batman vs the riddler theme. Here is my problem:
The Riddler has taken over Gotham City and is hiding out in secret location. In order to enter, Batman needs to solve the code to enter the base and find the Riddler. Will you help defeat the Riddler, Batman needs your help!
Using the resources given to you and techniques learned in class, use the clues left by the Riddler to get the code to help Batman enter the secret hide out.
[The resource would be base ten blocks of 100, 10 and 1 to help with grouping and a number line on graph paper to help with a visual. The clues left by the Riddler are: five numbers add to 100 (Clue 1), the difference between the greatest number and the lowest number is 12 (Clue 2), the numbers in the sequence cannot be the same (Clue 3), there are 2 codes (Clue 4). They would be on separate pages and you would explain to the students they cannot show there clues to another group member, they would have to verbally communicate with each other about their individual clues.]
I really hope the class enjoyed the activity and had fun. Also my fellow class mates who presented also did a great job!
Finally, students need to see math as sensible (not something they don't need), useful (related to real life), and do-able (for confidence). We talked about what makes a good math problem and these words also fall under that category. Some other things that make a good problem are wide base, variable, engaging and entertaining.
Thanks for stopping by, catch you next week. :)
So today was my learning activity presentation. I had the topic of whole number operations. Honestly I was really nervous going first and all so I'm hoping it went well. Using what I learned in the class previous, and in other classes I am taking; I decided to gamify the topic and activity in order to grasp the attention of my fellow classmates. I related it to a real life situation (even though it was fictional) and based the question I had on that real life situation. I created a batman vs the riddler theme. Here is my problem:
The Riddler has taken over Gotham City and is hiding out in secret location. In order to enter, Batman needs to solve the code to enter the base and find the Riddler. Will you help defeat the Riddler, Batman needs your help!
Using the resources given to you and techniques learned in class, use the clues left by the Riddler to get the code to help Batman enter the secret hide out.
[The resource would be base ten blocks of 100, 10 and 1 to help with grouping and a number line on graph paper to help with a visual. The clues left by the Riddler are: five numbers add to 100 (Clue 1), the difference between the greatest number and the lowest number is 12 (Clue 2), the numbers in the sequence cannot be the same (Clue 3), there are 2 codes (Clue 4). They would be on separate pages and you would explain to the students they cannot show there clues to another group member, they would have to verbally communicate with each other about their individual clues.]
I really hope the class enjoyed the activity and had fun. Also my fellow class mates who presented also did a great job!
Also, this week in class we focused on multiple ways to express and show how to complete an equation. When doing subtraction we used two methods: compensation subtraction and constant difference.
The example of compensation subtraction is as follows:
547
-296
simply add 4 to each number you get
551
-300
251
The example of constant difference is as follows:
2002
- 467
when you take away 3 from each number you get
1999
- 464
1535
Using these methods you can make equations simpler and easier to follow along and understand the key concepts of subtraction.
We also talked about the different ways to express 25 x 28. We can use an array to simplify the parts of the equation. Also shown in the picture below are the many different we can explain to a learner how to solve for 28 x 25.
Thanks for stopping by, catch you next week. :)
Subscribe to:
Posts (Atom)